USACO 2025 Feb Gold

1. Bessie's Function

important

Bessie 有一个特别的函数 $f(x)$，接收一个 $[1, N]$ 内的整数作为输入，并返回一个 $[1, N]$ 内的整数（$1 \le N \le 2 \cdot 10^5$）。她的函数 $f(x)$ 由 $N$ 个整数 $a_1 \ldots a_N$ 定义，其中 $f(x) = a_x$（$1 \le a_i \le N$）。

Bessie 希望这个函数是幂等的。换句话说，它应当对于所有整数 $x \in [1, N]$ 满足 $f(f(x)) = f(x)$。

Bessie 可以以代价 $c_i$ 将 $a_i$ 的值修改为 $[1, N]$ 内的任意整数（$1 \le c_i \le 10^9$）。求 Bessie 使 $f(x)$ 变为幂等所需要的最小总代价。

• 测试点 $1$: $N \le 20$。
• 测试点 $2\sim 7$: $a_i \ge i$。
• 测试点 $8\sim 13$: 所有 $a_i$ 各不相同。
• 测试点 $14\sim 19$: 没有额外限制。

除此之外，在后三个子任务中，前一半的测试点将满足对于所有 $i$ 有 $c_i=1$。

对于每个关系，$i \rightarrow A[i]$，我们建一条从 $i$ 指向 $A[i]$ 的边。最终会得到若干个连通分量，对每个连通分量来说，每个节点有且仅有一条出边，因此，我们得到的是一颗内向基环树。因此，我们可以分别处理每个连通分量，最后再将答案相加即可。

若节点 $i$ 的出边指向其自身（即 $a_i = i$），则称该节点为不动点，在数学上，即为满足条件 $f(x) = x$ 的点。

幂等条件

所有的 $i$，$i$ 和 $a_i$ 其中之一必须是不动点。

注意

如果需要修改节点 $i$ 的出边，那最优策略是将节点 $i$ 指向其自身，即修改 $i$ 为不动点（设置 $a_i = i$）。这是因为修改的代价总是 $c_i$，我们修改节点 $i$ 的指向节点，不会增加其他节点的成本，如果修改 $a_i = i$ 后，任何指向 $i$ 的节点都会满足幂等条件。

注意

本题等价于将图中的点进行染色，保证每条边上的端点至少有一个点被染色，求最小代价。

子任务1（$N \le 20$）

枚举黑色节点的集合，再检查是否题目要求。时间复杂度 $O(2^n\times n)$。

参考代码

#include <bits/stdc++.h>
using namespace std;

const int N = 25;
int n, A[N], B[N], C[N];

int main() {
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> A[i];
  for (int i = 1; i <= n; i++) cin >> C[i];
  memcpy(B, A, sizeof A);
  long long ans = LLONG_MAX;
  for (int stat = 0; stat < (1 << n); stat++) {
    memcpy(A, B, sizeof B);
    long long sum = 0;
    for (int bit = 0; bit < n; bit++) {
      if (((stat >> bit) & 1) && A[bit + 1] != bit + 1) {
        sum += C[bit + 1];
        A[bit + 1] = bit + 1;
      }
    }

    bool flag = true;
    for (int i = 1; i <= n; i++) {
      if (A[i] != i && A[A[i]] != A[i]) {
        flag = false;
        break;
      }
    }
    if (flag) ans = min(ans, sum);
  }
  cout << ans << '\n';
}

子任务2 （$c_i=1$）

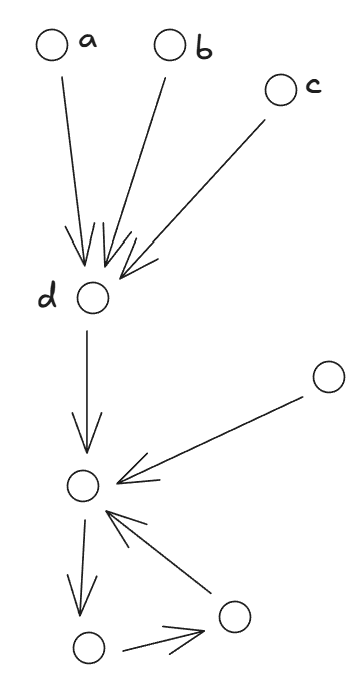
在修改节点的代价一样的条件下，我们可以贪心的对更有价值的点进行修改，对于边 $i \rightarrow A[i]$，要么节点 $i$ 为黑色，要么节点 $A[i]$ 为黑色， 在上图表示的情况下，对于边 $a \rightarrow d$、$b \rightarrow d$、$c \rightarrow d$，将 $d$ 染为黑色的成本最低。由此，我们给出下面通过拓扑排序实现的贪心策略：

选择任意一个入度为 0 且之前未被选择过的节点 $i$。如果 $i$ 或 $a_i$ 已经染色，则不需要进行任何操作。否则，我们将 $a_i$ 染色，成本为 $1$。然后删掉点 $i$，最后会剩下了一个环，换上一些点以及变为了黑色，将换上任意一条边断开开始计算成本，若起点已经被染色，则计算出的结果便是最优解。若起点未被染色，则分别计算起点染色和不染色的成本，取更小的值累加至总成本中。

参考代码

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
int n, A[N], C[N], in[N];
bool ok[N]; // 是不动点
bool ok2[N];
int main() {
  ios::sync_with_stdio(false);
  cin.tie(0);
  cin >> n;
  for (int i = 1; i <= n; i++) {
    cin >> A[i];
    in[A[i]]++;
    if (A[i] == i) ok[i] = true;
  }
  for (int i = 1; i <= n; i++) cin >> C[i];

  queue<int> q;
  for (int i = 1; i <= n; i++) {
    if (!in[i]) q.push(i);
  }

  int ans = 0;
  while (q.size()) {
    int x = q.front(); q.pop();
    in[A[x]]--;
    if (!in[A[x]]) q.push(A[x]);

    if (ok[x]) continue;
    if (ok[A[x]]) continue;
    ans++;
    ok[A[x]] = true;
  }

  memcpy(ok2, ok, sizeof ok);
  for (int i = 1; i <= n; i++) {
    if (!in[i]) continue;

    int j = i;
    int sum1 = 0;
    do {
      in[j]--;
      if (!ok[j] && !ok[A[j]]) ok[A[j]] = true, sum1++;
      j = A[j];
    } while (j != i);

    j = i;
    int sum2 = 0;
    if (!ok2[i]) ok2[i] = true, sum2 = 1;
    do {
      if (!ok2[j] && !ok2[A[j]]) ok2[A[j]] = true, sum2++;
      j = A[j];
    } while (j != i);
    ans += min(sum1, sum2);
  }

  cout << ans <<details endl;
}

子任务3 （$a_i \ge i$）

在此限制下，环的长度只能为 $1$，按照 「没有上司的舞会」 的方式进行处理即可。

设 $f(i, j)$ 表示使得节点 $i$ 对应的子树满足要求的最小成本。

• 若 $j = 0$，则节点 $i$ 本身被染色。
• 若 $j = 1$，则节点 $i$ 不被染色。

若节点 $i$ 被染色，那么 $i$ 的每个子节点是否被染色均满足条件关系。
$\displaystyle f(i, 1) = c_i + \sum_x \min (f(x, 0), f(x, 1))$

若节点 $i$ 不染色，那么 $i$ 的每个子节点均需被染色。
$\displaystyle f(i, 0) = \sum_x f(x, 1)$

因为根节点一定是被染过色的，所以最终结果为 $f(root, 1)$，实现的时候注意去掉根节点染色的成本。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;

int n, A[N], C[N];
bool v[N];
long long f[N][2];
vector<int> sons[N];

void dp(int x) {
    v[x] = true;
    for (auto y : sons[x]) {
        dp(y);
        f[x][0] += f[y][1];
        f[x][1] += min(f[y][0], f[y][1]);
    }
    f[x][1] += C[x];
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> A[i];
        if (A[i] != i) sons[A[i]].push_back(i);
    }
    for (int i = 1; i <= n; i++) {
        cin >> C[i];
        if (A[i] == i) C[i] = 0;
    }
    long long sum = 0;
    for (int i = 1; i <= n; i++) {
        if (v[i]) continue;
        int root = i;
        while (A[root] != root) root = A[root];
        v[root] = true;

        dp(root);
        sum += f[root][1];
    }
    cout << sum << '\n';
}

子任务4（$a_i$ 各不相同）

在此子任务中，图中只存在环，任选一条边 $i \rightarrow A[i]$，任意一种合法的方案要么 $i$ 被染色，要么 $A[i]$ 被染色，因此，我们可以将环从 $i \rightarrow A[i]$ 断开，计算 $i$ 作为被染色节点的最小代价，再将环从 $A[i] \rightarrow A[A[i]]$ 断开，计算将 $A[i]$ 作为被染色节点的最小代价。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;

int n, A[N], C[N];
bool v[N];
long long f[N][2];
int root;

void dp(int x, int root) {
  v[x] = true;
  if (x == root) {
    f[x][0] = 0;
    f[x][1] = C[x];
    return;
  }
  dp(A[x], root);
  f[x][0] = f[A[x]][1];
  f[x][1] = min(f[A[x]][0], f[A[x]][1]) + C[x];
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> A[i];
    for (int i = 1; i <= n; i++) {
      cin >> C[i];
      if (A[i] == i) C[i] = 0;
    }

    long long ans = 0;
    for (int i = 1; i <= n; i++) {
        if (v[i]) continue;
        long long res = 0;
        dp(A[i], i);
        res = f[A[i]][1];
        dp(A[A[i]], A[i]);
        res = min(res, f[A[A[i]]][1]);
        ans += res;
    }
    cout << ans << '\n';
}

完整解答

和子任务 4 一样，在环上任选一条边，将边上的两个端点分别作为根节点计算最优解即可。这里，利用了官方题解中找环上的点的方法。 在一个包含环的链表或函数图中，如果两个指针以不同的速度移动，快指针最终一定会从后面“追上”慢指针，两者在环内的某个位置相遇。 变量含义：

• x：慢指针，每次指向当前点的下一个点 $f(x)$。
• y：快指针，每次指向下下一个点 $f(f(y))$。

结果： 当 while 循环结束时，x（或 y）所指向的节点一定位于该连通分量的环上。

参考代码

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;
int n, A[N], C[N];
vector<int> sons[N];
long long f[N][2];
int root;
bool v[N];

void dp(int x) {
  v[x] = true;
  f[x][0] = f[x][1] = 0;
  for (auto son : sons[x]) {
    if (son == root) continue;
    dp(son);
    f[x][0] += f[son][1];
    f[x][1] += min(f[son][0], f[son][1]);
  }
  f[x][1] += C[x];
}

int main() {
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> A[i], sons[A[i]].push_back(i);
  for (int i = 1; i <= n; i++) {
    cin >> C[i];
    if (A[i] == i) C[i] = 0;
  }
  long long ans = 0;
  for (int i = 1; i <= n; i++) {
    if (v[i]) continue;
    int x = i, y = A[i];
    while (x != y) {
      x = A[x], y = A[A[y]];
    }
    root = x;
    dp(root);
    long long res = f[root][1];
    root = A[x];
    dp(root);
    res = min(res, f[root][1]);
    ans += res;
  }
  cout << ans << endl;
}

2. The Best Subsequence

The Best Subsequence

Farmer John 有一个长为 $N$ 的位串（$1 \leq N \leq 10^9$），初始时全部为零。

他将首先按顺序对字符串执行 $M$ 次更新（$1 \leq M \leq 2 \cdot 10^5$）。每次更新会翻转从 $l$ 到 $r$ 的每个字符。具体地说，翻转一个字符会将其从 $0$ 变为 $1$，或反之。

然后，他会进行 $Q$ 次查询（$1 \leq Q \leq 2 \cdot 10^5$）。对于每个查询，他要求你输出由从 $l$ 到 $r$ 的子串中的字符组成的长为 $k$ 的字典序最大子序列。如果你的答案是一个位串 $s_1s_2 \dots s_k$，则输出 $\sum_{i=0}^{k-1} 2^i \cdot s_{k-i}$（即将其解释为二进制数时的值）模 $10^9+7$ 的余数。

一个字符串的子序列是可以从中通过删除一些或不删除字符而不改变余下字符的顺序得到的字符串。

我们知道，字符串 $A$ 的字典序大于长度相等的字符串 $B$，当且仅当在第一个 $A_i \neq B_i$ 的位置 $i$ 上（如果存在），我们有 $A_i > B_i$。

• 测试点 $1$：$N \leq 10, Q \leq 1000$。
• 测试点 $2$：$M \leq 10$。
• 测试点 $3\sim 4$：$N, Q \leq 1000$。
• 测试点 $5\sim 9$：$N \leq 2 \cdot 10^5$。
• 测试点 $10\sim 17$：没有额外限制。

子任务 4

$n \le 2 \times 20^5$

本题是先处理完所有的修改，再进行查询操作。因此，对所有的修改操作，可以利用差分进行保存，修改完成以后，再利用依次前缀和操作还原。

在一个长度为 len 的 $01$ 序列，要得到长度为 $k$ 且字典序最大的子序列，那么，需要在原序列中删掉 $len - k$ 个字符。

贪心策略

要使得字典序最大，那么需要尽可能删掉靠前的 $0$ 字符。

在本任务的参考代码中，我们使用了前缀和加二分来快速定位最后一个删除的 $0$ 的位置。

参考代码

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10, mod = 1e9 + 7;
int n, m, q;
int A[N], sum[N];
long long pre[N];

long long qpow(int a, int b) {
  long long base = a, ans = 1;
  while (b) {
    if (b & 1) ans = ans * base % mod;
    base = base * base % mod;
    b >>= 1;
  }
  return ans;
}

int main() {
  cin >> n >> m >> q;
  for (int i = 1; i <= m; i++) {
    int l, r; cin >> l >> r;
    A[l] ^= 1, A[r + 1] ^= 1;
  }

  for (int i = 1; i <= n; i++) {
    A[i] ^= A[i - 1];
    sum[i] = sum[i - 1] + A[i];
    pre[i] = (pre[i - 1] * 2 + A[i]) % mod;
  }
  for (int i = 1; i <= q; i++) {
    int l, r, k; cin >> l >> r >> k;
    if (sum[r] - sum[l - 1] >= k) {
      cout << qpow(2, k) - 1 << '\n';
      continue;
    }
    int len = r - l + 1;
    int lo = l - 1, hi = r;
    while (lo < hi) {
      int mid = lo + hi >> 1;
      if (mid - l + 1 - (sum[mid] - sum[l - 1]) < len - k) lo = mid + 1;
      else hi = mid;
    }
    long long ans = (qpow(2, sum[lo] - sum[l - 1])  - 1)* qpow(2, r - lo) % mod;
    ans += pre[r] - pre[lo] * qpow(2, r - lo) % mod;
    ans = ((ans % mod) + mod) % mod;
    cout << ans <<details '\n';
  }
}

完整解答