「提高 - 84」割点和桥
给出无向连通图 :
桥
若对于 ,从图中删去边 之后, 分裂为两个不相连的子图,则称 为 的桥或者割边。
割点
若对于 ,从图中删去节点 以及所有与 关联的边之后, 分裂成两个或两个以上不相连的子图,则称 为 的割点。
下面的图中,哪些边是桥,哪些点是割点呢?
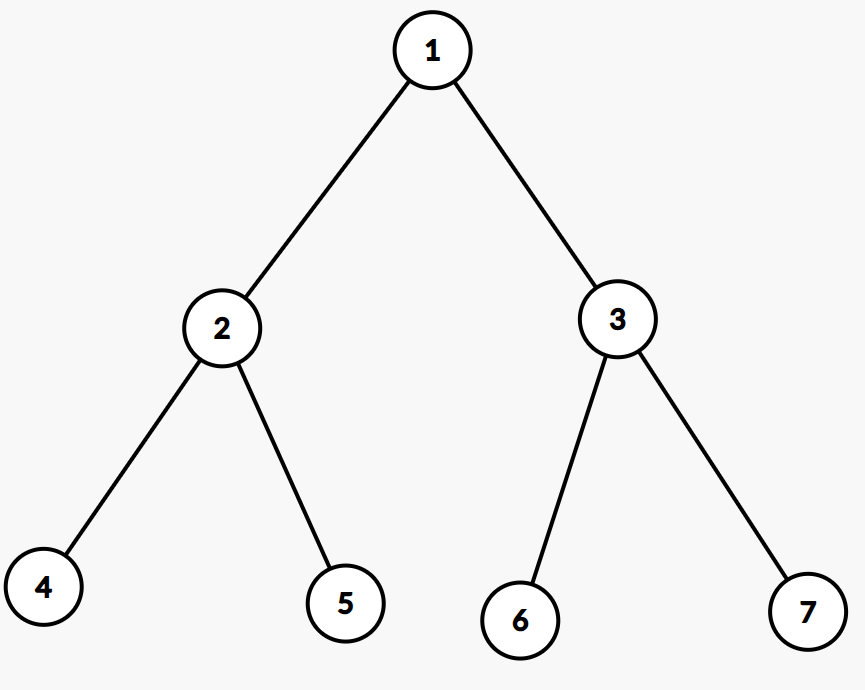


通过观察,我们可以看到若图为一棵树,那么每条边都是割边,每个非叶子的节点和儿子节点不只一个的根节点都是割点。
搜索树
在无向连通图中,从任意一个节点出发进行深度优先遍历,每个点只访问一次,所有发生递归的边构成了一棵树,我们称其为“图的搜索树”。如果图不连通的话,那么得到的为每一个连通块的搜索树组成的“搜索树森林”。
树边和回边
对于无向连通图来说,所有的非树边一定连接的是节点和其祖先节点。这样的边称为“回边“。
下图给出了一张无向连通图的搜索树的树边(红色)和回边(绿色)。
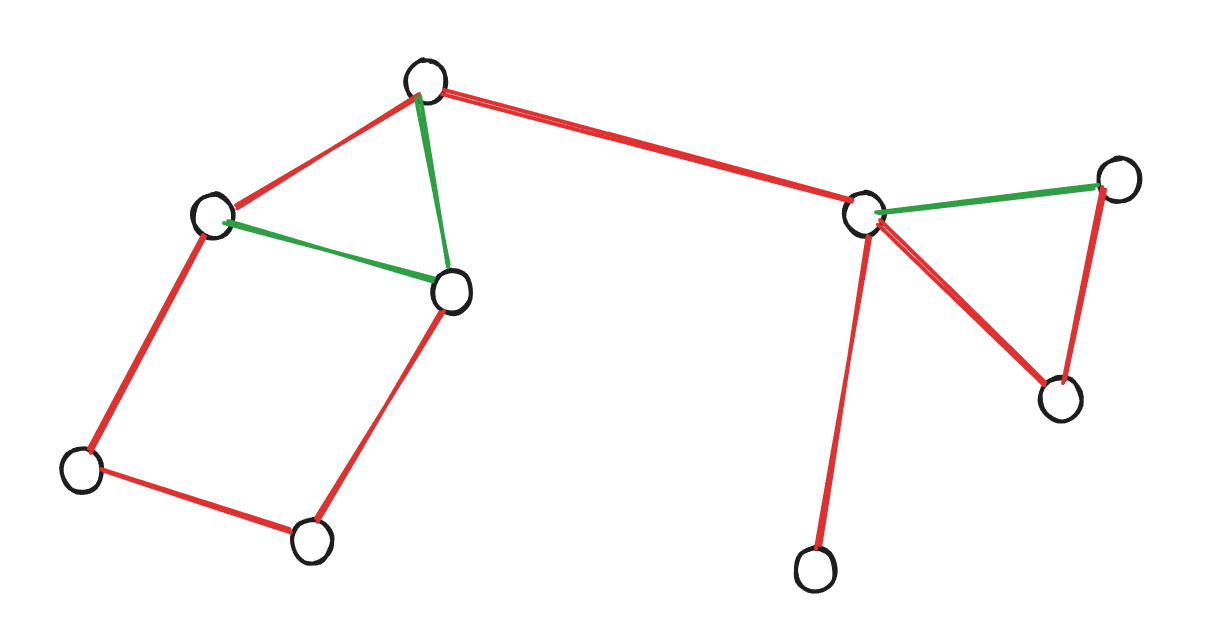
时间戳
在执行深度优先遍历的过程中,按照每个节点第一次被访问的顺序,依次将 个节点用 的整数标记,该标记称为 ”时间戳“,一般用数组 (Discovery Time)记录该值。
追溯值
为了分析删掉一条边或者一个点以后,图是否依然保持连通,我们引入追溯值的概念。
我们用 (Lowest Link) 表示从点 或者以 为根的 DFS 子树中任意一点出发,不经过到达 的父边,能够到达的具有最小 dfn 值的点的 dfn 值。节点的 low 值称为追溯值。
追溯值求解过程
在 DFS 遍历过程中,当访问到点 的时候。
- 执行操作 low[x] = dfn[x]
- 枚举 的出边 。
- 若 未曾访问过,递归访问 ,结束以后利用 更新 的追溯值,这是因为 能访问到的点 也可以访问到。
- 若 曾经访问过,且边 不是 的父边, 可直接回到时间戳更小的节点 ,故可通过 更新 的追溯值。
情况1, 的儿子节点 可以不经过其父边到达更早访问过的节点。
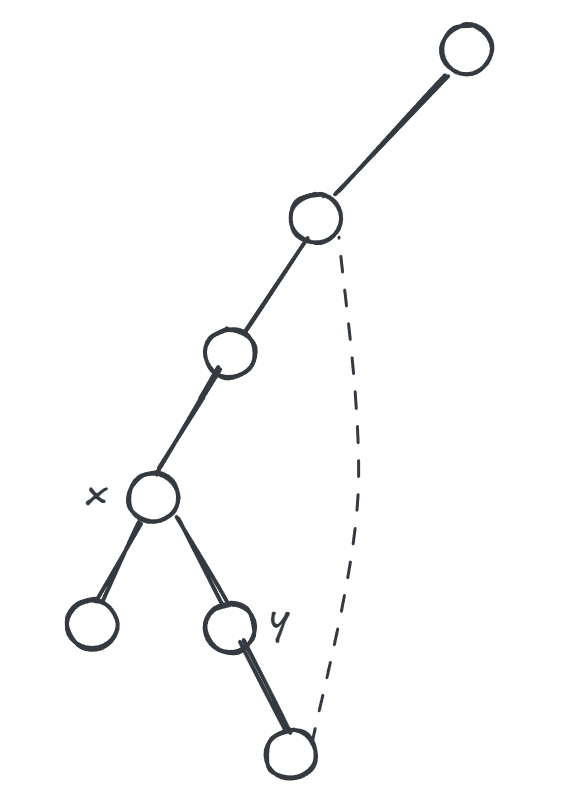
情况2, 本身 可以不经过其父边到达更早访问过的节点。
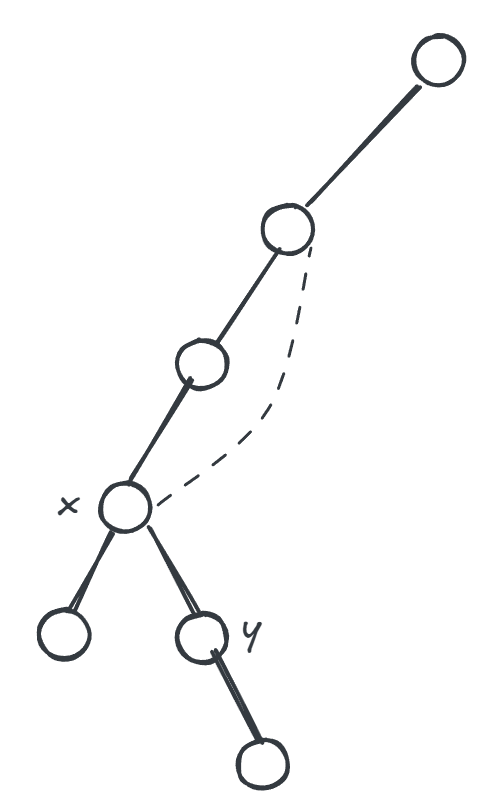
割边判定法则
无向边 是桥,当且仅当 是搜索树上的边且满足 。
证明
- 是桥,说明删掉边 以后, 不在与 所在的连通块连通,图中的边除了树边便是回边,所有 无法到达 或者 的祖先。 所以有 。
- ,说明不经过 的父边, 无法到达 或 的祖先节点,那么删掉边 之后, 将不再与 所在的连通块连通,所以 是桥。
值得注意的一个地方是,我们在枚举 的出边 的时候,一定要保证 不是 的父边,否则会错误的更新 的 low 值。
如上图,如果我们在递归到 的时候,错误的利用 的 dfn 值将 的 low 值更新为了 。那么,当回溯到节点 的时候,会发现不满足 dfn[y] < low[x],从而认为边 不是割边。
无向图求割边参考代码
const int SIZE = 100010;
int head[SIZE], ver[SIZE * 2], Next[SIZE * 2];
int dfn[SIZE], low[SIZE], n, m, tot, num;
bool bridge[SIZE * 2];
void add(int x, int y) {
ver[++tot] = y, Next[tot] = head[x], head[x] = tot;
}
void tarjan(int x, int in_edge) {
dfn[x] = low[x] = ++num;
for (int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if (!dfn[y]) {
tarjan(y, i);
low[x] = min(low[x], low[y]);
if (low[y] > dfn[x])
bridge[i] = bridge[i ^ 1] = true;
}
else if (i != (in_edge ^ 1))
low[x] = min(low[x], dfn[y]);
}
}
int main() {
cin >> n >> m;
tot = 1;
for (int i = 1; i <= m; i++) {
int x, y;
scanf("%d%d", &x, &y);
add(x, y), add(y, x);
}
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i, 0);
for (int i = 2; i < tot; i += 2)
if (bridge[i])
printf("%d %d\n", ver[i ^ 1], ver[i]);
}
割点判定法则
割点的判定需按照节点是否是根节点分情况讨论。
- 若 不是根节点,则 是割点等价于存在 的子节点 满足 。
- 若 是根节点,则 是割点等价于 的子节点至少有两个。
因为割点判定法则是小于等于号,所以在求割点时,不必考虑父节点和重边的问题,从 出发能访问到的所有点的时间戳都可以用来更新 。
上面这段话来自算法进阶指南,我理解的是这会使得所有节点的 low 值都会小于等于其父节点的 dfn 值,但因为判断条件是 ,所以不会影响判断结果。
const int SIZE = 100010;
int head[SIZE], ver[SIZE * 2], Next[SIZE * 2];
int dfn[SIZE], low[SIZE], stack[SIZE];
int n, m, tot, num, root;
bool cut[SIZE];
void add(int x, int y) {
ver[++tot] = y, Next[tot] = head[x], head[x] = tot;
}
void tarjan(int x) {
dfn[x] = low[x] = ++num;
int flag = 0;
for (int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x]) {
flag++;
if (x != root || flag > 1) cut[x] = true;
}
} else low[x] = min(low[x], dfn[y]);
}
}
int main() {
cin >> n >> m;
tot = 1;
for (int i = 1; i <= m; i++) {
int x, y;
scanf("%d%d", &x, &y);
if (x == y) continue;
add(x, y), add(y, x);
}
for (int i = 1; i <= n; i++)
if (!dfn[i]) root = i, tarjan(i);
for (int i = 1; i <= n; i++)
if (cut[i]) printf("%d ", i);
puts("are cut-vertexes");
}
相关题目
例1 BLO
城有 个城镇, 条双向道路。每条道路连结两个不同的城镇,没有重复的道路,所有城镇连通。把城镇看作节点,把道路看作边,容易发现,整个城市构成了一个无向图。
你需要输出 个整数,其中第 个整数表示把与节点 关联的所有边去掉之后 (不去掉节点 本身),无向图中有多少个有序点对 ,满足 和 不连通。
若 不是割点,按照割点的定义,删掉点 以后和与之相连的边以后,剩余的点依然保持连通,因此,只有点 和其余点之间是不连通的,此时对答案的贡献为 。
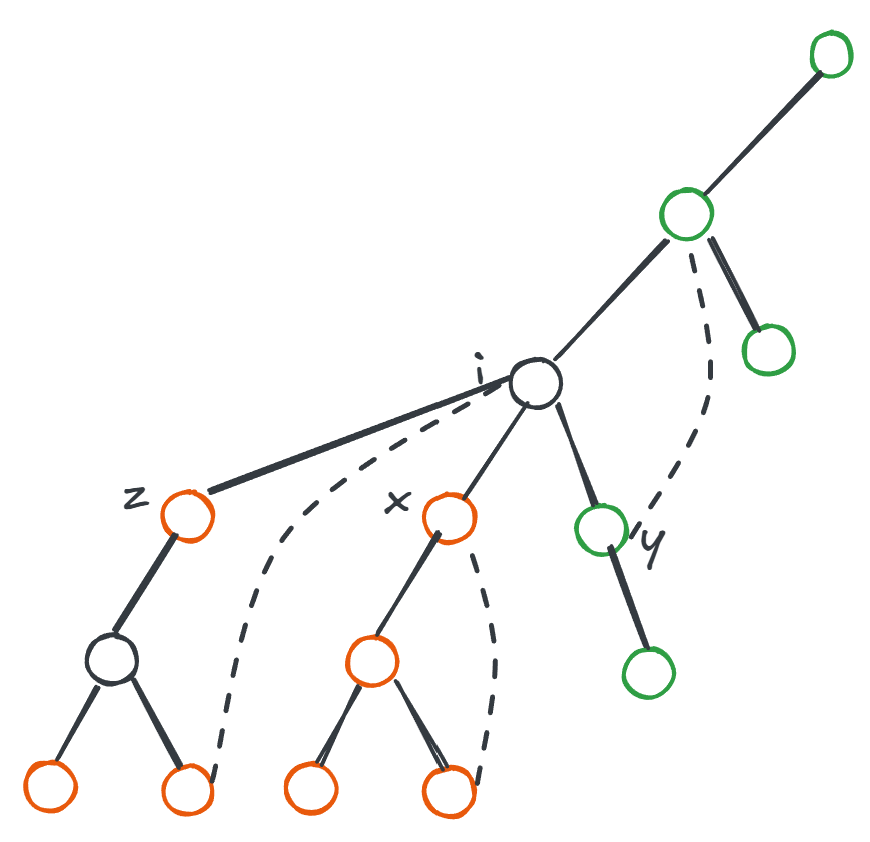
若 是割点, 的子节点可以分为两类:
- 满足 的子节点
这类节点在删掉 出发的边以后, 的子树包含的节点将不再与其他节点连通。记这些节点为 - 满足 的子节点
这类节点以及其子树包含的节点将与子树 以及 之外的节点构成一个连通块。
总的来说,在 是割点的条件下,删掉 出发的边以后,节点会分为 个连通块,分别是子树 包含的节点,节点 ,和剩余的节点。 那么,在一个连通块任选一个点,和不在该连通块的点都不连通。设子树 的节点数量为 。
此时,对答案的贡献为:
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 500010;
int head[N], ver[M * 2], Next[M * 2];
int dfn[N], low[N], Size[N];
long long ans[N];
bool cut[N];
int n, m, tot, num;
void add(int x, int y) {
ver[++tot] = y; Next[tot] = head[x], head[x] = tot;
}
void tarjan(int x) {
dfn[x] = low[x] = ++num; Size[x] = 1;
int flag = 0, sum = 0;
for (int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if (!dfn[y]) {
tarjan(y);
Size[x] += Size[y];
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x]) {
flag++;
ans[x] += (long long)Size[y] * (n - Size[y]);
sum += Size[y];
} else low[x] = min(low[x], dfn[y]);
} else low[x] = min(low[x], dfn[y]);
}
if (x != 1 || flag > 1) cut[x] = true;
if (cut[x])
ans[x] += (long long)(n - sum - 1) * (sum + 1) + (n - 1);
else
ans[x] = 2 * (n - 1);
}
int main() {
cin >> n >> m; tot = 1;
for (int i = 1; i <= m; i++) {
int x, y;
scanf("%d%d", &x, &y);
if (x == y) continue;
add(x, y); add(y, x);
}
tarjan(1);
for (int i = 1; i <= n; i++)
printf("%lld\n", ans[i]);
return 0;
}
上面参考代码中
if (cut[x]) ans[x] += (long long)(n - sum - 1) * (sum + 1) + (n - 1);
else ans[x] = 2 * (n - 1);
在 不是割点的情况下,上面代码第一行中的 sum 自然为 ,依然等于 。故代码可以省掉关于 是否是割点的判断。
例2 Electricity 电力
求一个图删除一个点之后,联通块最多有多少。
-
若 是割点
我们把 删掉以后, 所在的连通块会分成若干个连通块。设 为 在搜索树上的子节点,并满足条件 ,那么删掉 以后,子树 包含的节点将构成一个连通块。最后,不满足 的子树和 的父侧子树将构成另一个连通块。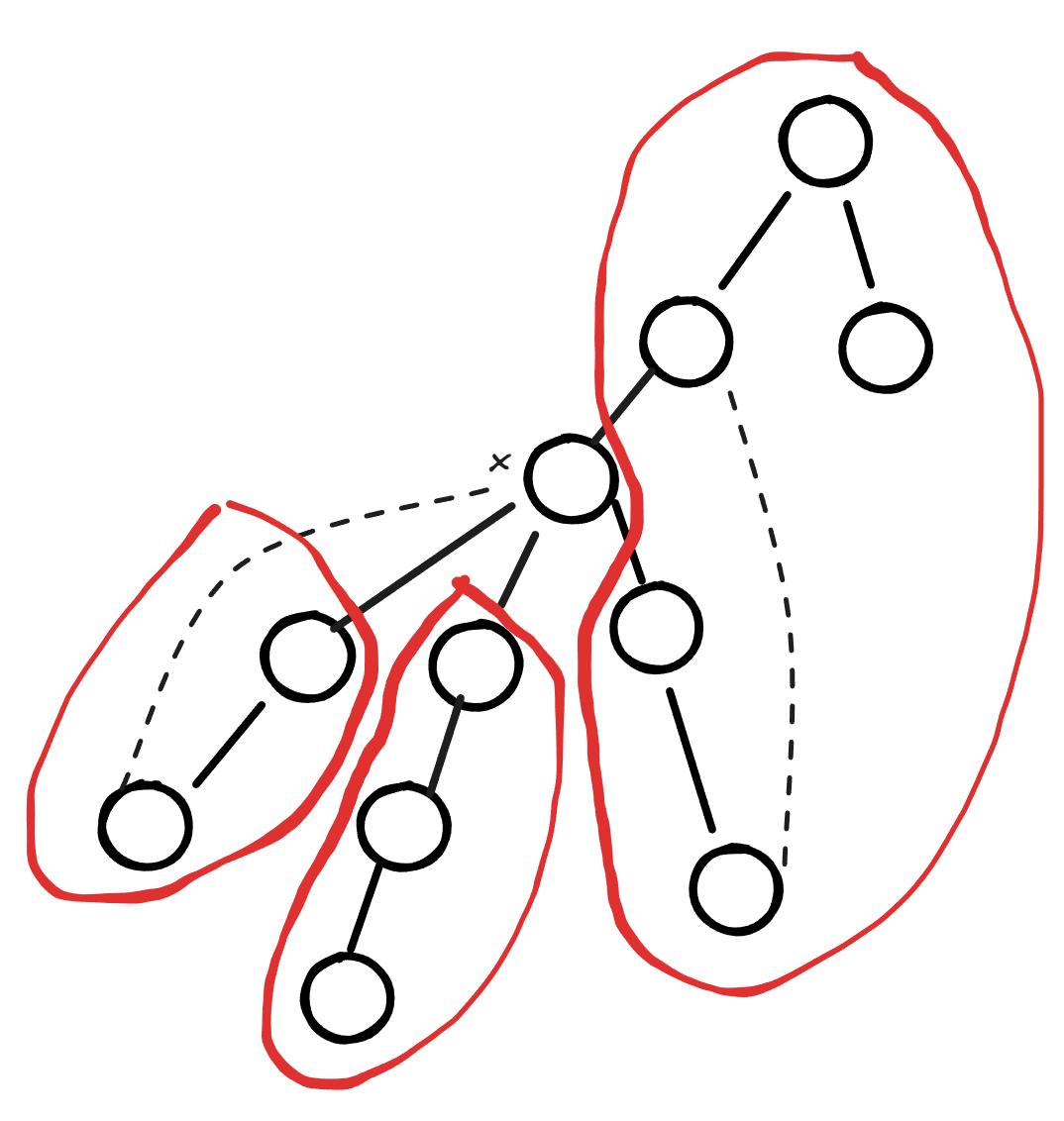
如上图所示,删掉割点 以后,图分成了 个连通块。值得注意的是,若 是根节点,那么, 的所有子节点 都满足 ,此时,分成的连通块数量即为 的子节点数量。
-
若 不是割点
我们把 删掉以后,若连通块仅有 一个节点,那么删掉 会得到 个连通块,否则,依然是一个连通块。在实现的时候,该部分结果与割点部分的代码计算结果一致,具体见参考代码。
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10000 + 5, M = 15e3 + 10;
int p, c;
int head[N], nxt[M << 1], ver[M << 1], tot;
int dfn[N], low[N], tim, c_tot, ans, flag, root;
bool cut[N];
void add(int x, int y) {
ver[++tot] = y, nxt[tot] = head[x], head[x] = tot;
}
void dfs(int x) {
dfn[x] = low[x] = ++tim;
int parts = 0;
for (int i = head[x]; i; i = nxt[i]) {
int y = ver[i];
if (!dfn[y]) {
dfs(y);
low[x] = min(low[x], low[y]);
if (dfn[x] <= low[y]) parts++;
} else low[x] = min(low[x], dfn[y]);
}
if (x != root) parts++;
ans = max(ans, pargs);
}
void solve() {
memset(dfn, 0, sizeof dfn);
memset(low, 0, sizeof low);
c_tot = 0;
ans = 0;
tot = 1;
memset(head, 0, sizeof head);
for (int i = 1; i <= c; i++) {
int p1, p2; cin >> p1 >> p2;
p1++, p2++;
add(p1, p2), add(p2, p1);
}
for (int i = 1; i <= p; i++) {
if (dfn[i]) continue;
root = i;
dfs(i);
c_tot++;
}
cout << ans + c_tot - 1 << endl;
}
int main() {
while (cin >> p >> c && p) solve();
}
例3 矿场搭建
煤矿工地可以看成是由隧道连接挖煤点组成的无向图。为安全起见,希望在工地发生事故时所有挖煤点的工人都能有一条出路逃到救援出口处。于是矿主决定在某些挖煤点设立救援出口,使得无论哪一个挖煤点坍塌之后,其他挖煤点的工人都有一条道路通向救援出口。
请写一个程序,用来计算至少需要设置几个救援出口,以及不同最少救援出口的设置方案总数。
倘若删掉的是割点,那么得到的每一个连通块都要保证至少一个出口,因此,我们找到图的所有割点。去掉割点后的连通块视为一个整体(点双连通分量)。如下图所示:
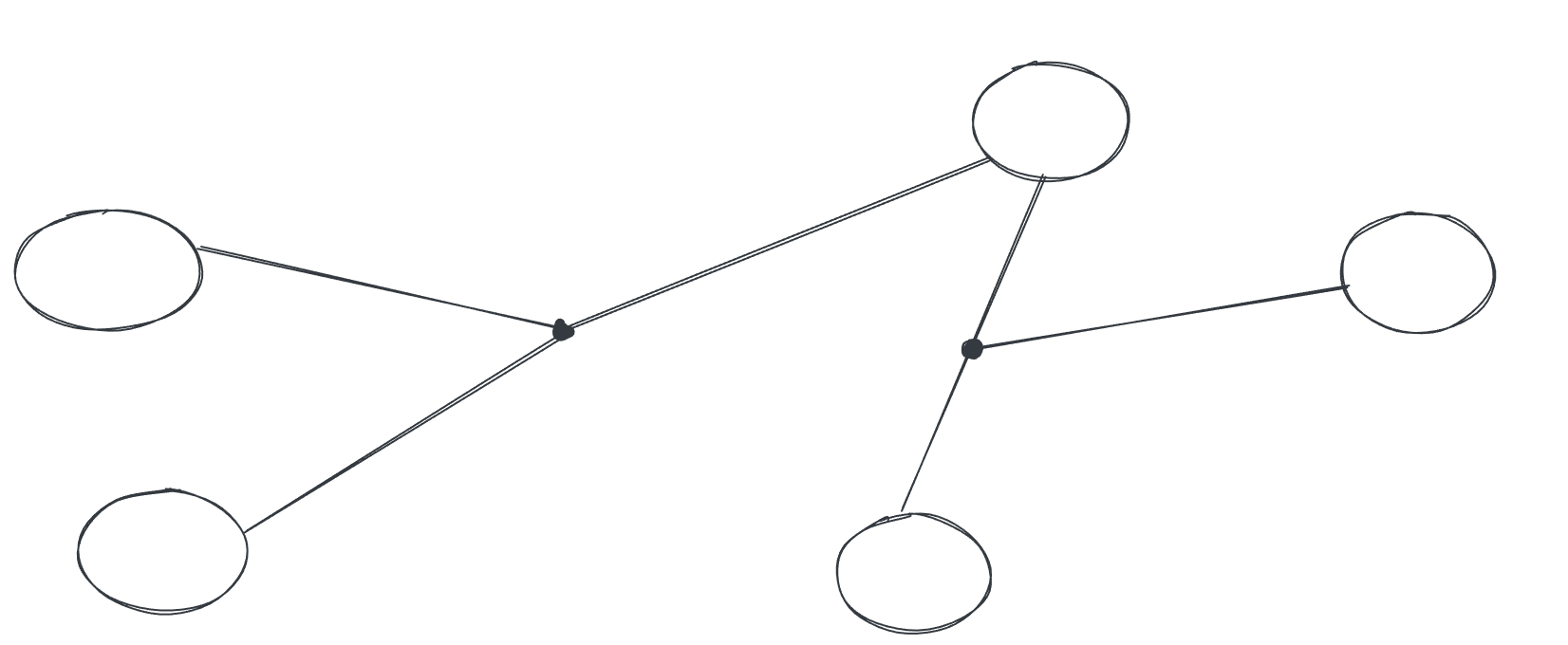
- 每个只和一个割点相连的连通块,必须设置一个出口,方案数量为该连通块的点的数量。
- 如果一个连通块和多个割点相连,那么该区域不需要设置出口,因为即使删掉一个割点,也能从其他路线出逃。
因此,删掉所有割点,统计所有只和一个割点相连的连通块的节点数量,需要设置的出口数量为这些连通块的数量,方案数为这些连通块的节点数量的乘积。
注意特殊情况,若整个图不存在割点,那么需要设置两个出口,这样才能保证如果删掉了一个设置出口的节点,可以从另一个出口逃出。方案数量为 。
具体实现时,首先求出所有割点,接下来,从每个未曾访问过的非割点开始搜索,统计每个连通块的节点数量,以及和本连通块相连的割点数量,更新答案。
#include <bits/stdc++.h>
using namespace std;
const int N = 200 + 5, M = 500 + 10;
int head[N], ver[M << 1], nxt[M << 1], tot;
int m;
int dfn[N], low[N], tim;
bool cut[N];
int tot_cut;
int v[N];
int ans1;
long long ans2;
void add(int x, int y) {
ver[++tot] = y, nxt[tot] = head[x], head[x] = tot;
}
void tarjan(int x) {
dfn[x] = low[x] = ++tim;
int flag = 0;
for (int i = head[x]; i; i = nxt[i]) {
int y = ver[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
if (dfn[x] <= low[y]) {
flag++;
if (x != 1 || flag > 1) tot_cut++, cut[x] = true;
}
} else low[x] = min(low[x], dfn[y]);
}
}
void bfs(int t) {
queue<int> q;
q.push(t);
v[t] = t;
int sum = 1, connect_cut = 0;
while (q.size()) {
int x = q.front(); q.pop();
for (int i = head[x]; i; i = nxt[i]) {
int y = ver[i];
if (v[y] == t) continue;
if (cut[y] && v[y] != t) { v[y] = t; connect_cut++; continue; }
v[y] = t, sum++;
q.push(y);
}
}
if (connect_cut == 1) ans1++, ans2 *= sum;
}
int main() {
int Case = 0;
while (cin >> m && m) {
tot = 1;
memset(head, 0, sizeof head);
memset(v, 0, sizeof v);
memset(cut, 0, sizeof cut);
memset(low, 0, sizeof low);
memset(dfn, 0, sizeof dfn);
tot_cut = 0;
Case++;
int n = 0;
tot = 1;
for (int i = 1; i <= m; i++) {
int s, t; cin >> s >> t;
add(s, t), add(t, s);
n = max({n, s, t});
}
tarjan(1);
ans1 = 0, ans2 = 1;
if (tot_cut == 0) {
ans1 = 2, ans2 = n * (n - 1) / 2;
} else {
for (int i = 1; i <= n; i++) {
if (!v[i] && !cut[i]) {
bfs(i);
}
}
}
printf("Case %d: %d %lld\n", Case, ans1, ans2);
}
}
例4 嗅探器
给出一无向图连通图,以及图上的两点 和 ,求删掉哪个点以后,可使得 、 分别位于不同的连通块?
所求点 为割点,且删掉 之后,、 分别位于不同的连通块。
因此,我们从点 开始执行 tarjan 求割点算法,如果找到的割点位于 到 的路径中,那么该割点便满足条件。
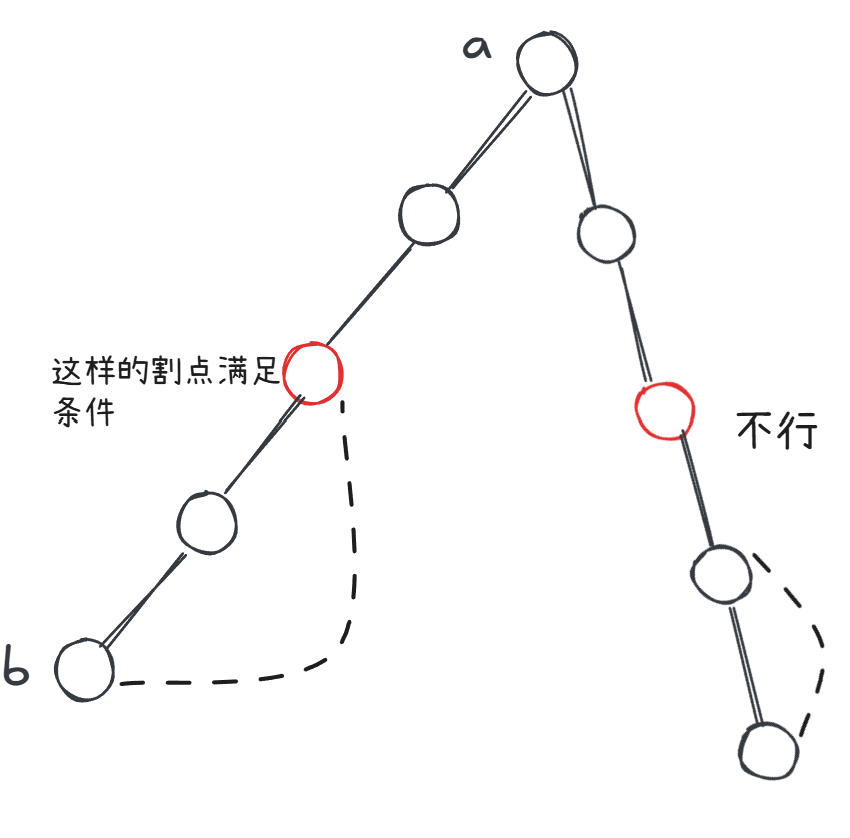
如何保证割点 位于 、 之间的路径呢?假设我们是通过 的儿子节点为 判定 为割点,那么,若满足条件
便意味着 位于 、 之间。这是因为 的值不是 ,说明已经搜过点 ,其值大于等于 ,说明先访问的 ,再访问的 。所以 一定位于子树 。