「04」离散化
离散化是指将一个大范围的集合中的元素和小范围的集合的元素建立起一一对应的关系,用小范围的元素来替代大范围的元素,从而实现降低空间复杂度和时间复杂度的作用。
例如:对集合 进行离散化操作。我们只需进行排序和去重的两步操作,便可以完成离散化。
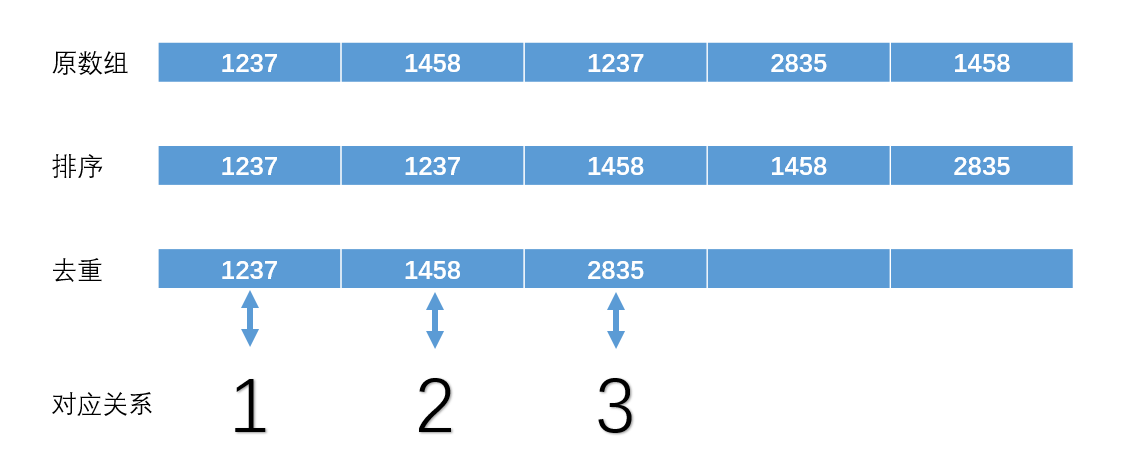
实现
数组+手动去重
int A[N], m;
void discrete() {
sort(A + 1, A + n + 1);
for (int i = 1; i <= n; i++)
if (i == 1 || A[i] != A[i - 1])
A[++m] = A[i];
}
int query(int x) { // 查询 x 映射为哪个 1~m 之间的整数
return lower_bound(A + 1, A + m + 1, x) - A;
}
数组 + unique 函数(推荐)
int m; // 待离散化的数组中不重复元素的个数
void discrete() { // 离散化
sort (A + 1, A + n + 1);
m = unique(A + 1, A + n + 1) - (A + 1); // 去重
}
int query(int x) { // 查询元素 x 映射为 1 ~ m 中的哪一个元素
return lower_bound(A + 1, A + m + 1, x) - A;
}
vector + unique 函数
vector<int> A;
void discrete() { // 离散化
sort(A.begin(), A.end());
A.erase(unique(A.begin(), A.end()), A.end()); // 去重
}
int query(int x) { // 查询元素 x 映射为 A 中第几个元素
return lower_bound(A.begin(), A.end(), x) - A.begin();
}
相关题目
例1. Cinema
Cinema
有 部正在上映的电影,每部电影的语音和字幕都采用不同的语言,用一个 int 范围内的整数来表示语言。有 个人相约一起去看其中一部电影,每个人只会一种语言,如果一个人能听懂电影的语音,他会很高兴;如果能看懂字幕,他会比较高兴;如果语音和字幕都不懂,他会不开心。请你选择一部电影让这 个人一起看,使很高兴的人最多。若答案不唯一,则在此前提下再让比较高兴的人最多,。
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m, A[N], B[N], C[N], cnt[N], T[N], t;
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> A[i], T[i] = A[i];
sort(T + 1, T + n + 1);
t = unique(T + 1, T + n + 1) - T - 1;
auto query = [](int x) -> int {
int k = lower_bound(T + 1, T + t + 1, x) - T;
if (k > t || T[k] != x) return 0;
return k;
};
cin >> m;
for (int i = 1; i <= m; i++) cin >> B[i];
for (int i = 1; i <= m; i++) cin >> C[i];
for (int i = 1; i <= n; i++) cnt[query(A[i])]++;
int ans = 1, very_happy = 0, quite_happy = 0;
for (int i = 1; i <= m; i++) {
int b = query(B[i]), c = query(C[i]);
if (cnt[b] > very_happy || cnt[b] == very_happy && cnt[c] > quite_happy)
ans = i, very_happy = cnt[b], quite_happy = cnt[c];
}
cout << ans << endl;
}
例2. 区间和
区间和
假定有一个无限长的数轴,数轴上每个坐标上的数都是 。
现在,我们首先进行 次操作,每次操作将某一位置 上的数加 。
接下来,进行 次询问,每个询问包含两个整数 和 ,你需要求出在区间 之间的所有数的和。
, , ,
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int A[N], t;
int sum[N];
int query(int x) {
return lower_bound(A + 1, A + t + 1, x) - A;
}
int main() {
int n, m; cin >> n >> m;
vector<pair<int, int>> add;
for (int i = 1; i <= n; i++) {
int x, c; cin >> x >> c;
add.push_back({x, c});
A[++t] = x;
}
sort(A + 1, A + t + 1);
t = unique(A + 1, A + t + 1) - (A + 1);
for (auto [x, c] : add) sum[query(x)] += c;
for (int i = 1; i <= t; i++) sum[i] += sum[i - 1];
for (int i = 1; i <= m; i++) {
int l, r; cin >> l >> r;
l = query(l), r = query(r + 1) - 1;
cout << sum[r] - sum[l - 1] << '\n';
}
}